Cape Fear Academy, Wilmington, NC, 28412
This research would not have been possible without the exceptional guidance and support of my astrophysics mentor Dr. William Waller (IAU/OAE — National Astronomy Education Coordinator; The Galactic Inquirer Co-founder and Co-editor).
Abstract:
I investigated the statistical properties of Fast Radio Bursts (FRBs) with the aim of better understanding the possible source(s) of these mysterious outbursts. My study focused on the CHIME/FRB Catalog 1 database, whose self-consistent sensitivities and time resolutions would enable more robust statistics. The 474 single-burst and 61 repeating-burst sources were examined in terms of their locations on the sky, dispersion measures, burst durations, and fluences. According to the CHIME/FRB Catalog 1, the FRB population was evenly distributed in the northern sky so there is the likelihood that the sources are extragalactic in origin, rather than local to the Milky Way. The dispersion measures (DMs) are 3-8 times greater than those of galactic pulsars. This difference requires explaining in terms of their greater distances and/or local electronic environments. The DMs and other examined properties of single-burst vs. repeating FRBs are similar within the statistical uncertainties; therefore, the two source types cannot be clearly distinguished using this database. The timescale of the shortest burst durations binds the size of the bursting sources to less than half Earth’s radius. The independence of the bursting process with respect to its electronic environment is indicated by the lack of correlation between the burst duration and the dispersion measure. The frequency distribution of fluences indicates a pattern of rapid rise and extended fall-off with increasing fluence. The slope of the fall-off in the log-log frequency distribution (and corresponding power-law exponent) is flatter than that expected from a uniformly distributed population of FRBs. The dispersion measures do not correlate with the distant-dependent fluences, suggesting more local influences on the DMs.
Introduction and Background:
Fast Radio Bursts (FRBs) represent a new cosmic phenomenon of unknown origin. They have been detected since 2006 and yet remain a great mystery (The CHIME/FRB Collaboration, 2021). Fast Radio Bursts are flashes of radio emission lasting for several milliseconds. The time of arrival of signals depends on the radio frequency, called the dispersion measure (DM), which depends on the environment through which the signals travel, specifically the number of free electrons in their path. Very few FRBs have matches with sources observed at other wavelengths (Wikipedia – Fast Radio Burst). Some FRBs are associated with galaxies, while a very small sample has been identified with magnetars — quickly rotating highly-magnetic neutron stars in outburst. Some astronomers think that most FRBs are caused by magnetars, but there’s only a handful of magnetars known in our Milky Way galaxy, and they all seem too tame to be causing these extreme signals (Cooper, 2020). One FRB seems to have been in the same location as a known gamma-ray burst. This match suggests that FRBs could require more energy input than is typical of magnetar outbursts. To date, six gamma-ray bursts have been identified as flaring magnetars — two in the Milky Way galaxy and four more in the nearby galaxies M31, M81, M83 and NGC 253 (Sanders, 2021). Meanwhile, consistent match-ups between GRBs and FRBs remain to be established.
In my research, I examine the statistical properties of FRBs as gleaned from the CHIME/FRB Catalog 1. The CHIME radio telescope is uniquely suited as an FRB “discovery machine” which will be described first. I then explore the CHIME database in terms of the FRBs’ spatial distribution, DMs, time durations, and fluences. The DMs, in particular, appear to be uniquely high compared to those of pulsars, which merits further interpretation. Lastly, I consider whether or not the repeating FRBs represent a distinct population of burst characteristics. Prior researchers have claimed separate populations for the single-burst vs. repeating FRBs (Williams, 2020).
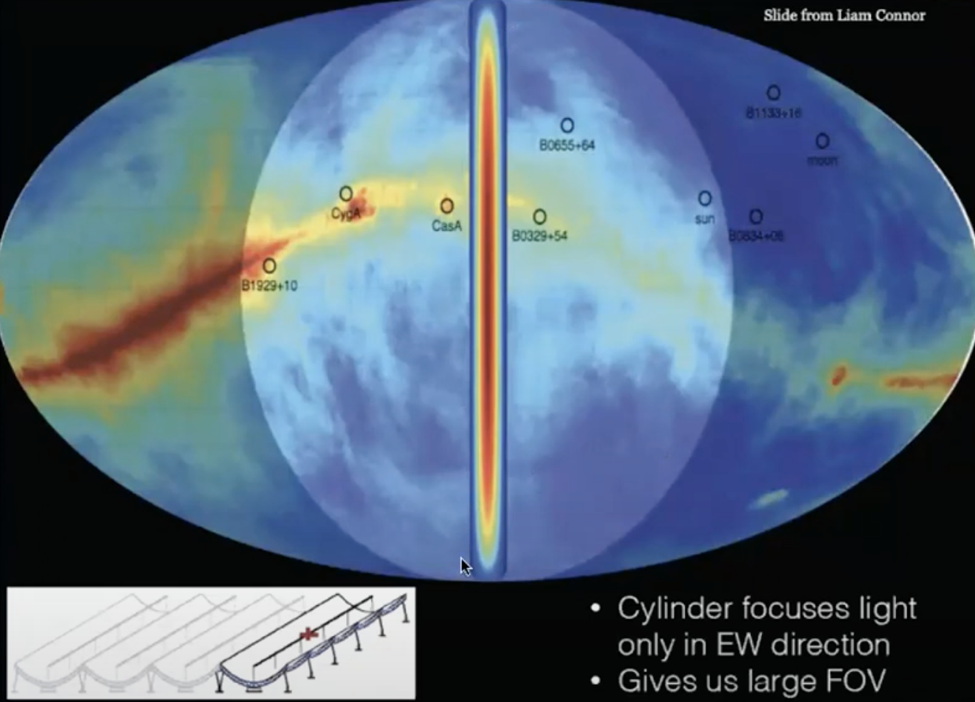
The CHIME Radio Observatory as an FRB Discovery Machine:

The CHIME Radio Observatory is located at the Dominion Radio Astrophysical Observatory in British Columbia, Canada (see Figure 1). It is operated by the National Research Council of Canada as a national facility for astronomy. The CHIME telescope is very unique since it consists of four long cylinders that cast a really long beam on the sky. So, as the earth rotates, the entire sky moves through the beam once per day. This is a really effective way of detecting FRBs. Firstly, the cylinder focuses light only in the E-W direction. This attribute enables the telescope to scan the space closely and in neat order (see Figure 2). Secondly, the CHIME telescope gives us a large field of view. In this way, the telescope can collect abundant information about the Fast Radio Bursts. Lastly, software relating the signal detections from each cylinder allows for subsequent location of sources within the long beam (see Figure 3).

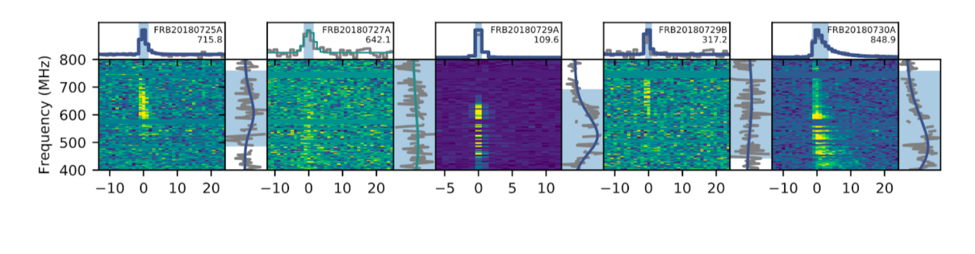
CHIME tracks the time of arrival vs. frequency of each burst. The slope of these plots provides the dispersion measure (DM) which is directly related to the number of free electrons along the line of sight according to …
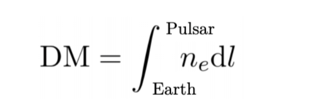
where the standard units for DM are in cm-3 pc (see Figure 4). These electrons interact with the radio signal, altering its propagation as a function of frequency. DMs for galactic pulsars are typically less than 200 cm-3 pc (see Figure 5).

The CHIME/FRB Catalog 1:
The data that have been applied in this research is from the CHIME/FRB Catalog 1. The data for this catalog were obtained between July 25, 2018 and July 1, 2019. They were made publicly available in June 2021, with an announcement on June 9 at the summer meeting of the American Astronomical Society. This catalog records all the Fast Radio Bursts that have been detected by the CHIME telescope. So far, the CHIME telescope has detected 535 FRBs in total, including 474 single-burst FRBs and 61 repeating FRBs from 18 sources (see Figure 6). This catalog increases the total number of publicly known FRBs by a factor of four (The CHIME/FRB Collaboration 2021).
Sticking with this database is very advantageous due to the CHIME observing facility having the same observing configuration with the same sensitivity and time resolution. In this way, the statistical properties of this research paper will be more robust. Therefore, the CHIME/FRB Catalog 1 provides a uniquely important resource for understanding FRB populations.
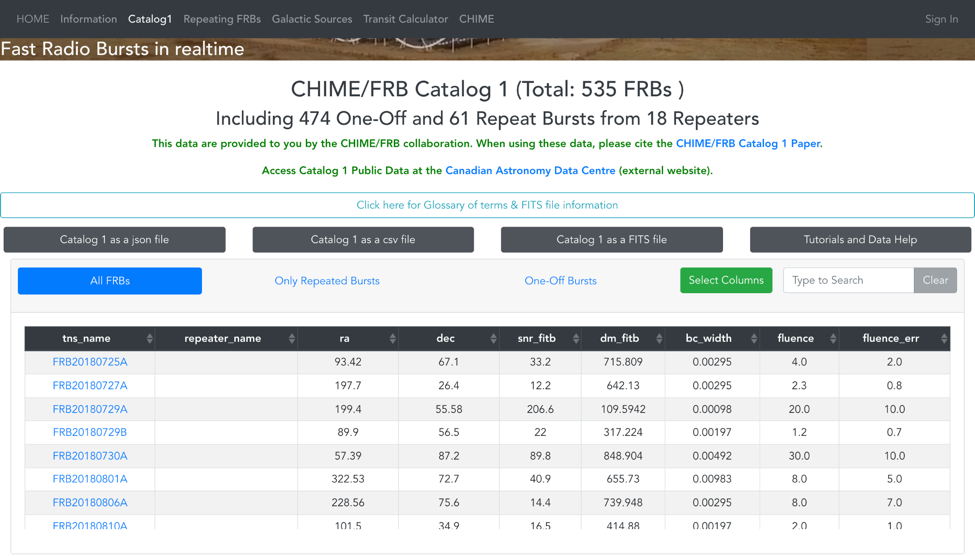
In the database, each Fast Radio Burst has been introduced by its TNS name, Right Ascension (RA) in degrees, Declination (Dec) in degrees, signal-to-noise ratio (SNR) as determined using the fitting algorithm fitburst, dispersion measure (DM) in units of pc cm-3, Boxcar width of the pulse in units of seconds, Fluence in units of Jy ms, and Fluence error in Jy ms. About 40 other parameters were also tabulated in the catalog; however, I have decided to focus on the statistics pertaining to the location in the sky, dispersion measure, pulse duration, and fluence for this particular study.
Statistical Analysis of FRB Properties:
I used Google sheets to tabulate the data and make plots of the various FRB properties. These include frequency distributions (histograms) of one property and scatter plots relating two properties.
Locations in the sky:
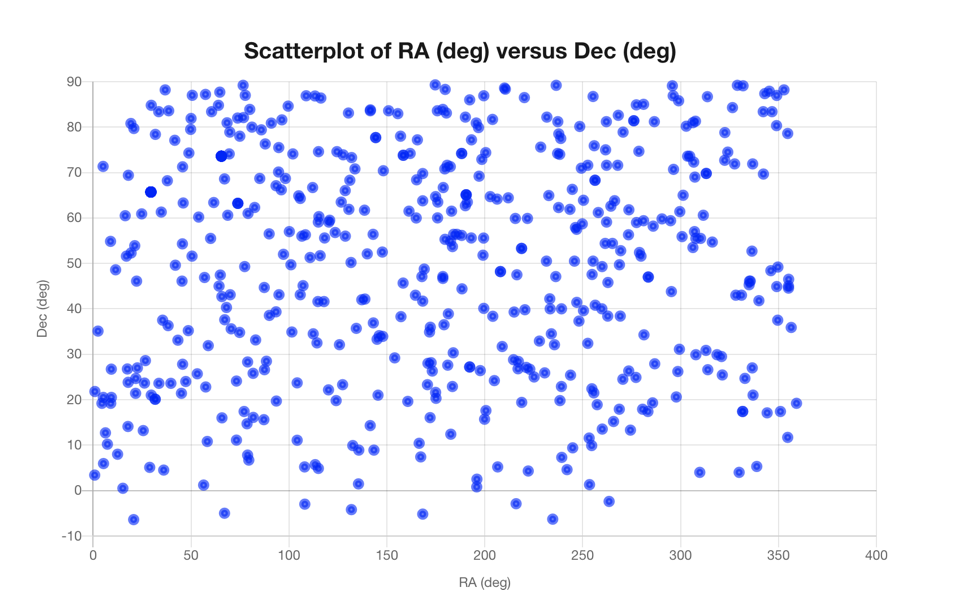
Figure 7 shows the spatial distribution of the detected FRBs on the sky, where equatorial coordinates of Right Ascension (RA) and Declination (Dec) are used. We can see that the range of declination is from -10 degrees to +90 degrees. This limited range is because the CHIME facility is located in British Columbia, Canada at a latitude of 49 degrees, so it is unable to detect sources more south than -10 degrees. Also, from this graph, we know that the locations are evenly spread out with no clustering or skewness, so we can know that the FRB sources do not stick to the disk of the Milky Way. Most likely the sources are extragalactic, instead of residing in the Milky Way.
Dispersion Measures:
As previously noted, the dispersion measure (DM) of a radio source is obtained from the slope of the corresponding frequency vs. time plot. The DM depends on the number of free electrons along the line of sight to the source. Figure 8 shows the distributions of dispersion measures for single-burst and repeating FRBs.


The dispersion measures in both FRB populations are factors of 3 to 8 times greater than those of the pulsars in our Milky Way galaxy (DM ~ 100 cm^-3 pc). This important finding could be the result of electron-rich environments associated with the FRBs. Young supernova remnants or other outbursting nebular phenomena could explain these high DMs. The notion of the local electronic environment affecting the FRB dispersion measures leads to the possibility of a “magnetar wind nebula” as a viable model (Margalit and Metzger, 2018). This model builds on the “pulsar wind nebula” model that has been proposed to explain certain behaviors of pulsars that are embedded in luminous nebulae (Yang and Dai, 2019).
Also, the graph shows a “positive” skewness towards lower dispersion measure. That is, most FRBs have a smaller dispersion measure and only a few have a larger dispersion measure (thus making a long “tail” at the higher DMs). It is unclear whether this skewness is the result of observational biases or rather the consequence of the actual FRB population and its environment. There is no discernable difference between the DM distributions of the single-burst and repeating FRBs.
Burst durations:
The CHIME/FRB Catalog 1 lists the burst duration for each FRB in terms of its “pulse width.” This timescale sets a spatial limit on the bursting source’s size, as it cannot exceed the light-travel distance set by d = c x t, where (c) is the speed of light and (t) is the burst duration. Figure 9 shows the distribution of burst duration for both single-burst and repeating FRBs. The dominant timescale is at the limits of the temporal resolution (<0.01s) giving an upper size limit of about 3,000 km — corresponding to half the radius of Earth.
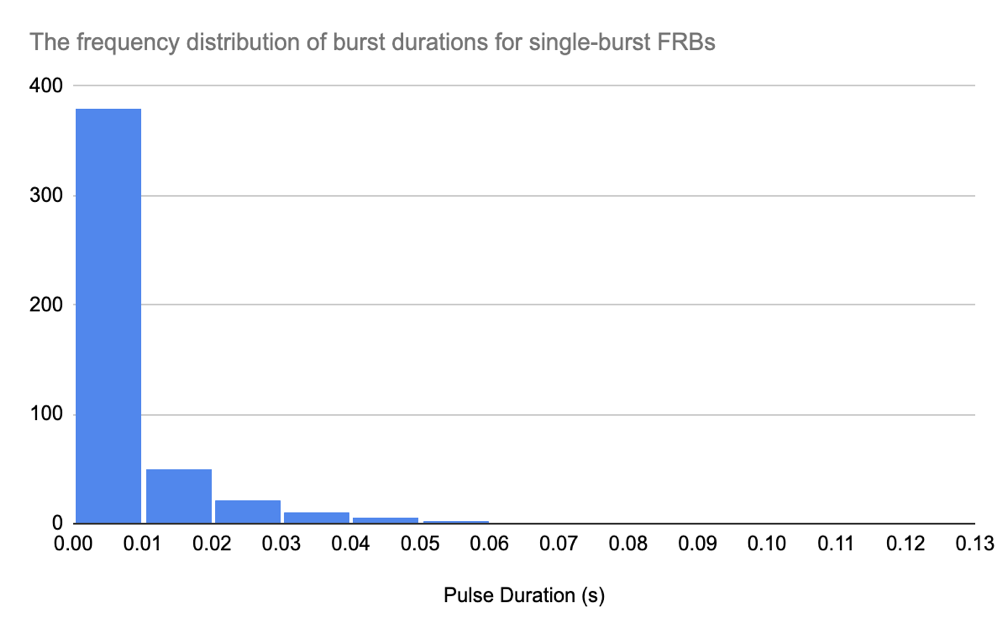
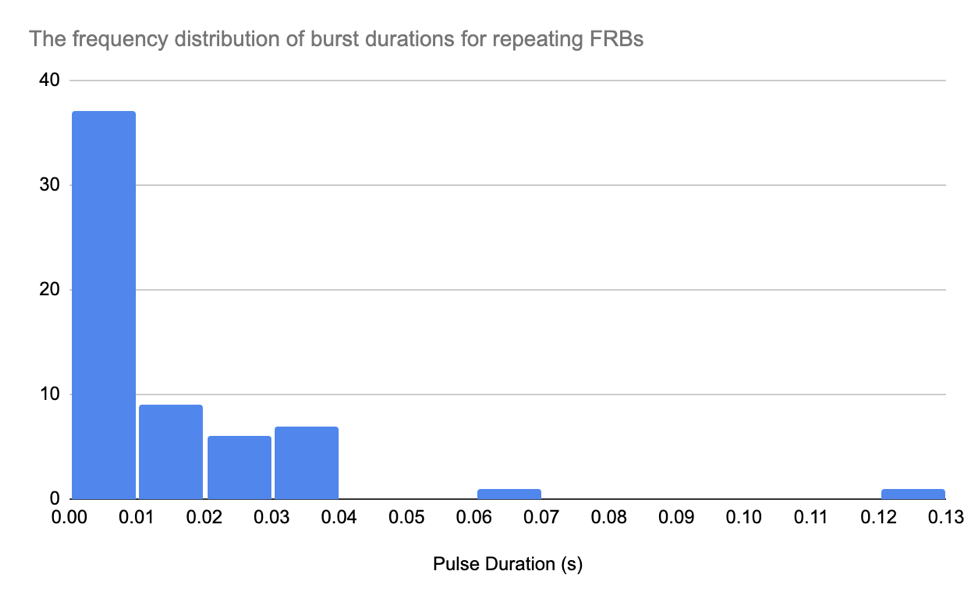
Both of these two distributions show a right-skewness, which means that the number of FRBs decrease with the increase of Pulse Duration. Also, the peak of these two distributions are in the interval between 0.00s to 0.02s. This shows that most FRBs do not exist for a long time. In this way, the telescopes with longer beams are very useful for detecting FRBs. The range for these two distributions appears to be the same (from 0.00s to 0.13s) so we can assume that the most FRBs do not exist longer than 0.13 s. Other investigators have found slightly greater pulse durations with the repeating FRBs (Williams, 2020).
Fluences:
The fluence of the burst is defined as the total energy that is released by a bursting source, which in the case of the CHIME/FRB Catalog 1, is the integral of the intensity (in Janskies) over the burst duration (in ms). Frequency distributions of fluence are shown in linear-linear, linear-log and log-log formats (see Figures 10-12). The linear-linear format (Figure 10) shows a preponderance of FRBs at the low fluence end (0-10 Jy-ms). The log-log format enables one to determine the slope (alpha) at the high fluence end (see Figure 12). This slope corresponds to the power of the N vs. Fluence relation (N = k x F[alpha]). (See Appendix A). The observed distribution of fluences suffers significantly from incompleteness at the low-fluence end. Considering only the high fluence counts (beyond F = 10 Jy-ms), one gets a slope for the log (counts) vs. log (fluence) points of (alpha = -0.77 [ repeating FRBs ] to -0.94 [ single burst FRBs ]). These values are significantly flatter than the value of -1.40 found by the CHIME/FRB Collaboration and the value of -1.50 expected from a spatially uniform distribution of sources (see Appendix A). I suspect that these differences can be attributed to significant incompleteness remaining even at these higher fluences. I did not attempt to account for this incompleteness, but the CHIME/FRB Collaboration modeled it extensively as part of its analysis.
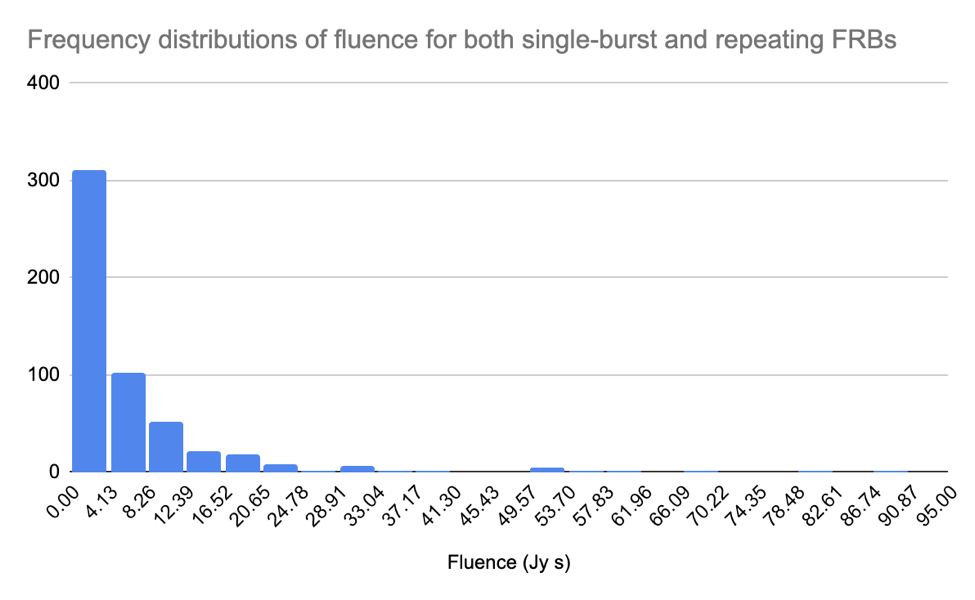
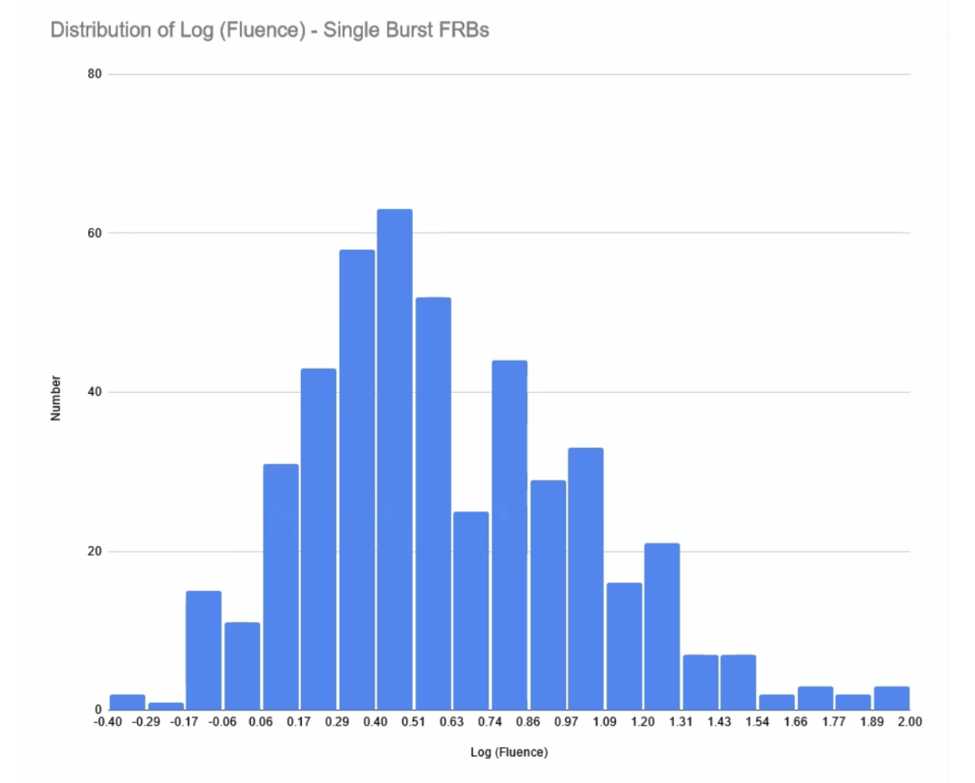
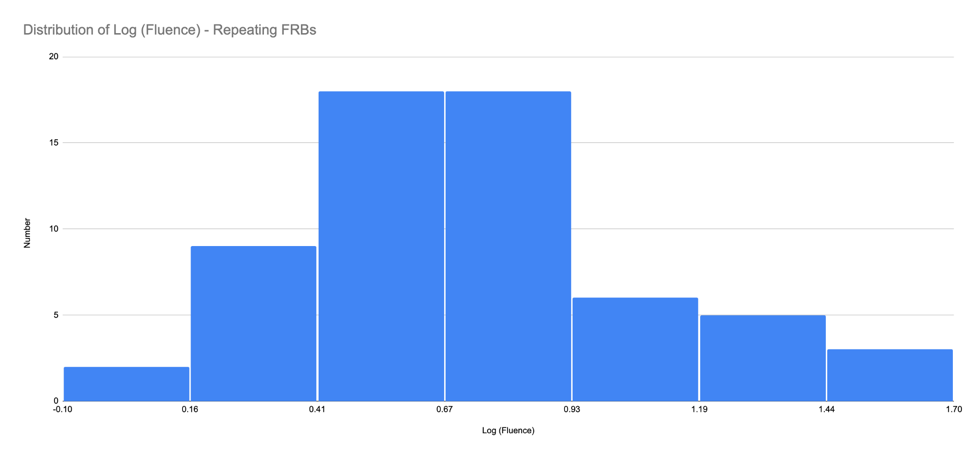
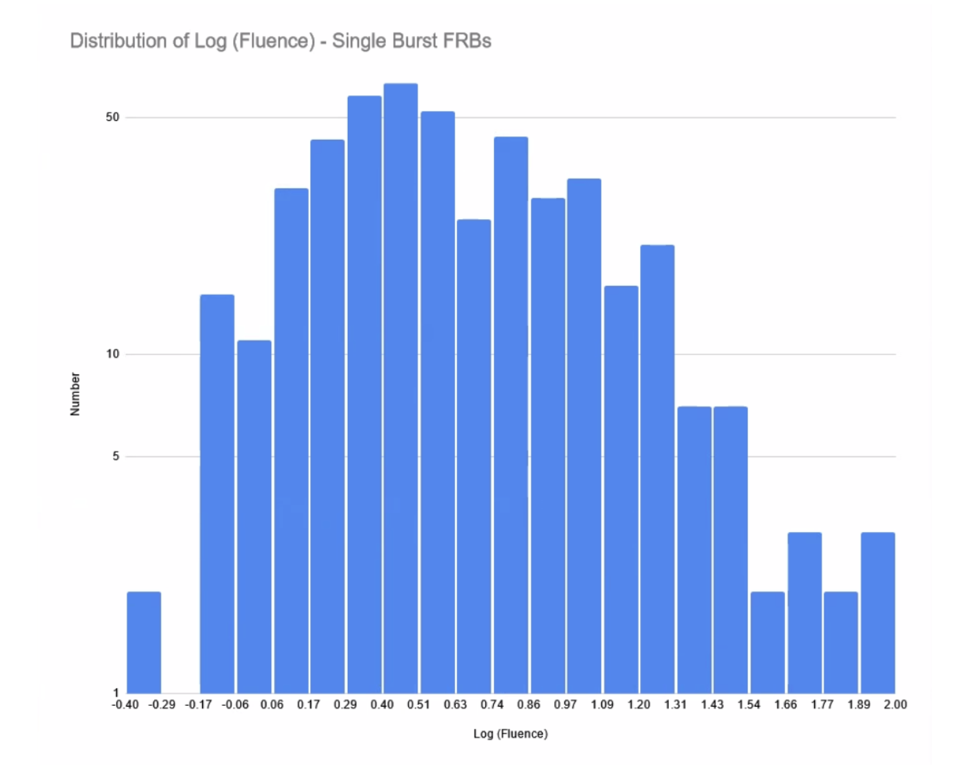
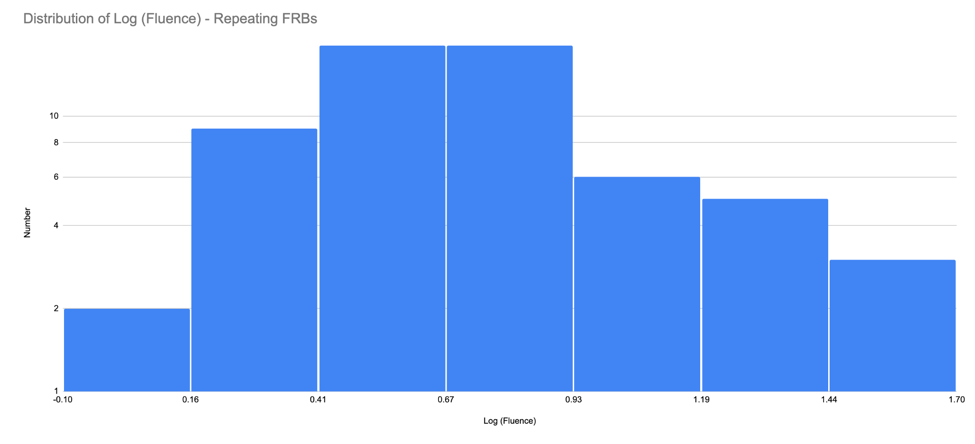
Figure 12b: The frequency distribution of fluence for repeating FRBs in log-log format.
In Figure 13, the dispersion measures are plotted against the fluences. The result is mostly a scatter diagram with negligible trends. If both quantities depend on distance, then there should be a correlation between the two — which is not evident. More likely, the dispersion measure is dependent on the source’s local environment of free electrons rather than on free electrons along the distance-dependent intergalactic medium. The upper bound of DMs does seem to decline with the fluence, however, suggesting a possible distance dependence on both quantities that is compromised by other influences.

Also noteworthy is that most of the data are clustered in the range of 0 to 10 (Jy-ms) fluence, which may show that the CHIME telescopes are sensitive to low fluences but may still suffer from incompleteness (see also Figures.10-12). Only at the higher fluences is the upper bound of DMs apparent, again suggesting a possible distance dependence where these brighter-appearing FRBs are likely at closer distances with correspondingly lower DMs.
Single-burst vs. Repeating FRB Populations:
Prior researchers have claimed differences between the single-burst vs. repeating FRB populations, such that the repeating FRBs have longer burst durations (Williams, 2020). These differences have been attributed to the repeating sources being local to the Milky Way galaxy. Within the limits of the statistics, I find no discernable difference between the properties of the single-burst vs. repeating FRB populations. The repeating FRBs suffer from low-number statistics, and so it is difficult to draw any robust conclusions about their uniqueness. As further FRBs are detected by CHIME and other radio telescopes, the statistics should improve to the point where any differences in the populations can be identified with greater confidence.
Conclusions and Discussion
I have accessed the CHIME/FRB Catalog 1 database and examined the statistical properties of the detected FRBs. This database is the largest collection of FRBs available. It is also self-consistent in terms of the observing configuration, sensitivity, and time resolution, thereby making the following statistical results more robust.
- The FRB population from the CHIME/FRB Catalog 1 is distributed uniformly across the northern sky. Therefore, it cannot be sourced to the disk of the Milky Way but rather is likely extragalactic in origin.
- The dispersion measures (DMs) are factors of 3 to 8 times greater than those of galactic pulsars. No difference in DMs is evident between the single-burst and repeating FRBs. The high dispersion measures in the CHIME/FRB Catalog 1 population need explaining.
- The distribution of burst durations has its peak with the shortest durations of 9 ms. This timescale constrains the size of the bursting sources to 2.7 x 106 m, or roughly 1/258 the diameter of the Sun, or half the Earth’s radius.
- The lack of correlation between the burst duration and the dispersion measure indicates that the bursting process is independent of its electronic environment.
- The distribution of fluences shows a rise and fall in counts with increasing fluence. The lower counts at the lower fluences can be ascribed to serious incompleteness due to sensitivity issues. The counts at the higher fluences can be modeled as a power law (N ~ fluence[alpha]) with a power of alpha = -0.94 for single bursts to alpha = -0.77 for repeaters. These powers are significantly flatter than alpha = -1.50 as expected from a uniformly distributed population of FRBs in Euclidean space.
- The dispersion measures do not correlate with the fluences. If the fluence is dependent on distance to the source, then this lack of correlation would suggest a lack of correlation between the DMs and distance. The upper bound of DMs declines with increasing fluence, however, which could be explained by a weak distance dependence competing with other more localized influences.
The unusually high dispersion measures in the FRB population are especially intriguing. One popular model is to place the FRBs at great cosmological distances so that the signals traverse large columns of free electrons. The feasibility of this model can be understood with the following example of an FRB source at a cosmological distance of 109 pc with its signal passing through an intergalactic medium with an average density of (1 – 10) particles/m3. After conversion of the density to (1 – 10) x 10-6/cm3, one gets a DM of (1 – 10) x 103 pc cm-3. Such a “strawman” estimate comes close to the DMs found in the CHIME/FRB Catalog 1 database.
An alternative model is to localize the free electrons to the FRB sources themselves, ie. in the form of a “magnetar wind nebula.” Such nebulae would be similar to the “pulsar wind nebulae” and supernova remnants that surround some neutron stars (ie. the Crab nebula). The pulsar wind nebula is a type of nebula sometimes found inside the shell of a supernova remnant (SNR). It is powered by winds generated by the central pulsar (Wikipedia — Pulsar wind nebula).
Consider a magnetar wind nebula of 1 pc radius and average density of 103 cm-3, akin to those of some pulsar wind nebulae (Straal, Connor, and van Leeuwen, 2020). Such nebulae could yield DMs as high as ~103 pc cm-3, consistent with the CHIME/FRB DMs.
Already, the database shows a lack of correlation between the DMs and the fluences. This suggests a lack of correlation between the DMs and distance to the sources, thus casting doubt on the IGM model. The declining upper bound of DMs with increasing fluence could be indicating some distance dependence that is competing with more localized influences associated with e.g. magnetar wind nebulae. Until we obtain a statistically robust population of FRBs with matches to galaxies of known distance, this doubt will remain. Meanwhile, the magnetar wind nebula model could be tested by searching for predicted counterparts at other wavelengths … e.g. soft X-rays, optical line emission, etc.
One promising approach would be to use the FAST radio telescope in China to search for quiescent emission from previously detected FRBs. FAST is the largest single-dish radio telescope in the world, with an angular resolution of 0.89 deg — 0.02 deg at 70 MHz — 3.0 GHz, respectively. It has already detected 201 pulsars (Anderson, 2021) but has detected only one FRB to date (Xu et al., 2021), probably because its beam is so small.Detection of quiescent radio emission and its characterization (ie. synchrotron vs. free-free emission) would help to constrain models of the FRB’s nebular environment.
Works Cited
Anderson, Natali. “FAST Radio Telescope Discovers 201 New Pulsars.” SCI News, 20 May 2021, www.sci-news.com/astronomy/galactic-plane-pulsar-snapshot-survey-09679.html
Collaboration, FRB, et al. “The First Chime/Frb Fast Radio Burst Catalog.” ArXiv.org, 8 June 2021, arxiv.org/abs/2106.04352.
Cooper, Keith. “Milky Way Magnetar Could Be the Source of a Fast Radio Burst.” Physics World, 5 Nov. 2020, physicsworld.com/a/milky-way-magnetar-could-be-the-source-of-a-fast-radio-burst/.
“Fast Radio Burst.” Wikipedia, Wikimedia Foundation, 13 July 2021, en.wikipedia.org/wiki/Fast_radio_burst.
“Frb-Web.” Chime, www.chime-frb.ca/catalog.
He, C., et al. “The Correlation between Dispersion Measure and x-Ray Column Density from Radio Pulsars.” The Astrophysical Journal, vol. 768, no. 1, 2013, p. 64., doi:10.1088/0004-637x/768/1/64.
Margalit, Ben, and Brian D. Metzger. “A Concordance Picture of FRB 121102 as a Flaring Magnetar Embedded in a Magnetized Ion-Electron Wind Nebula.” Astrophysical Journal Letters, Vol. 868, L4, 2018, https://iopscience.iop.org/article/10.3847/2041-8213/aaedad.
“Pulsar Wind Nebula.” Wikipedia, Wikimedia Foundation, 31 Oct. 2020, en.wikipedia.org/wiki/Pulsar_wind_nebula.
Sanders, R. “Astronomers find signature of magnetar outbursts in nearby galaxies,” Berkeley press release, January 2021, https://news.berkeley.edu/2021/01/13/astronomers-find-signature-of-magnetar-outbursts-in-nearby-galaxies/, and references therein.
Straal, S. M., et al. “A Dispersion Excess from Pulsar Wind Nebulae and Supernova Remnants: Implications for Pulsars and FRBs.” Astronomy & Astrophysics, vol. 634, 2020, doi:10.1051/0004-6361/201833376.
Williams, Matt. “Even More Repeating Fast Radio Bursts Discovered.” Universe Today, 25 Mar. 2020, www.universetoday.com/145440/even-more-repeating-fast-radio-bursts-discovered/.
Xu, H. et al., FAST FRB Key Project, “FAST detection and localization of FRB20201124A,” The Astronomer’s Telegram, No. 14518, April 2021, https://www.astronomerstelegram.org/?read=14518
Yang, Yu-Han, and Zi-Gao Dai. “Emission from a Pulsar Wind Nebula: Application to the Persistent Radio Counterpart of FRB 121102.” Astrophysical Journal, Vol. 885, p. 149, 2019, https://arxiv.org/pdf/1911.12833.pdf
Appendix A: Derivation of the Fluence Distribution in a Uniformly Populated Euclidean Universe
Consider the differential relation between source counts (N) and source fluence (F)
dN/dF = dN/dr * dr/dF, where (r) is the distance to the source.
If (N) goes as volume (V),
Then, ΔN = ΔV = Δr * 4πr2.
So ΔN/Δr = 4πr2
and dN/dr = 4πr2.
The received signal strength (fluence) is F = F0/4πr2
So r2 = F0/4πF
r = (F0/4πF)½ = F0 ½ * (4πF)-½
dr/dF = (-F0½ * F-3/2)/2(4π)1/2
dN/dF = dN/dr * dr/dF = (4πr2) (-F0½ * F-3/2)/2(4π)1/2 = (F0/F)(-F0½ * F-3/2)/2(4π)1/2
Simplifying yields
dN/dF = (-F03/2 /4π1/2) F-5/2
and taking the integral over the fluence, the relation between counts and fluence becomes
N = (-F03/2 /4π1/2) F-3/2)/(-3/2) + const.
Taking the natural logarithm of this relation yields
In N = In (2F03/2/4π1/2)/3 – 3/2 In F + const = ln (F03/2 / 6 π1/2) – 3/2 ln F + const,
where the expected slope (alpha) is -3/2 = -1.50. The same slope pertains when taking the base-ten logarithm as shown in Figure 12.
